

Golden items are considered very valuable and quite rare. To the answers, you have found an answer that is very close to what is sometimes known as the "golden mean". This is the type of strange phenomenon that intrigues mathematicians. Notice anything worth investigating further? Try finding the average of your answers. Try dividing each number into the number that follows it, e.g. If you investigate how the numbers of the sequence relate to each you will make another amazing discovery. All involve the Fibonacci numbers - if you would like to discover how and why, Dr Ron Knott has the answers for you. In branching plants, flower seeds and petal and leaf arrangements, on the outside of pineapples and inside apples as well as within pine cones. If you don't know about the rabbits you can find out more at Fibonacci's Three Wishes 2įibonacci's number sequence (1,1,2,3,5,8,etc) has been discovered in some very interesting places. But there was more to Fibonacci than a number pattern and counting breeding rabbits. There is an Fibonacci association and even a journal dedicated to the sequence. His statue is not as well known as his number sequence. Well, Leonardo is better known as Fibonacci. Do you recognise him now? (picture from the website of the School of Mathematics and Statistics University of St Andrews, Scotland) Whatever the case may be, it is interesting to note the presence of this ratio in so many varied forms in nature.Here a picture of a statute of Leonardo that is in his home city. Some claim that this is evidence of God’s presence and his intelligent design of the universe, whereas, at the same time, others point out that these are mere statistical manipulations. This ratio has been revered as divine, and called God’s fingerprint due to its presentation in numerous living as well as non-living entities. In addition to these examples, the divine proportions is also seen in various architectural wonders, like the Greek Parthenon, paintings like the Last Supper, in musical symphonies and instruments, and even in biblical texts (dimensions of Noah’s Ark). Head to navel ► Ratio of the length of each digit of a finger ► Shoulder to fingertip.Golden ratios that are observed in the human body are as follows: ► Insects: The ratios of the body segments (head, thorax, and abdomen) to each other are golden sections. ► Tiger: Almost all the facial features and their positions show golden sections, including the ratio of the length and breadth of the face. ► Penguins: The ratio of the position of the body markings at the eyes, beak, and wings, in contrast with its total height. ► Dolphins: Dimensions (length:breadth) of eyes, fins, as well as tail section. Despite this vast range, they still exhibit the divine proportion in various parts of their bodies. Golden Ratio RepresentationĪnimals show a wide range of body structures.
FIBONACCI RECTANGLE SERIES
This value approaches closer to the golden ratio as the series progresses. The interesting aspect of this series is that, after the first four to five numbers, if each number is divided by its immediate predecessor, it yields a value close to 1.618. The initial sequence is as follows – 0, 1, 1, 2, 3, 5, 8. This sequence is a series of numbers, where each number is the sum of its two preceding numbers. This value can be derived using basic quadratic equations, geometry, or by analyzing the Fibonacci sequence. Its mathematical value is 1.61803398… For general purposes, the value is assumed to be 1.618. This ratio is called the golden ratio, and is signified by the Greek letter phi (Φ).
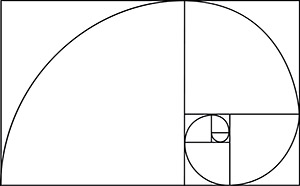
A more accurate way to describe it would be, to call it a ratio of line segments when a line is divided into two parts (a and b), such that the ratio of ‘a’ to ‘b’ is the same as the ratio of (a+b) to ‘a’. All these names point to the fact that, it is a ratio of dimensions of a given entity, but this description seems vague. The golden ratio is referred to by many diverse terms, such as golden mean, golden section, medial section, divine proportion, golden cut, and extreme and mean ratio.

The first we may compare to a measure of gold the second we may name a precious jewel.” ―Johannes Kepler “Geometry has two great treasures: one is the Theorem of Pythagoras the other, the division of a line into extreme and mean ratio.


 0 kommentar(er)
0 kommentar(er)
